Automated Market Makers (AMMs): Math, Risks & Solidity Code
TL;DR: Automated Market Makers (AMMs) in DeFi
- AMMs use math, not order books, to set prices and enable 24/7 trading on-chain.
- Constant product formula (x*y=k) powers Uniswap and most DEXs (ensures liquidity but causes price impact and impermanent loss).
- Liquidity providers (LPs) deposit up to two tokens (e.g ETH, USDC) into a pool, enabling users to swap between them while LPs earn fees, but have risk of impermanent loss if token prices diverge.
- Key risks: Price impact, slippage, impermanent loss, and arbitrage.
- Best practices: Understand the math, use secure code, and always compare LP fees to potential losses.
History & Motivation: Why AMMs?
Traditional exchanges use Central Limit Order Books (CLOBs) to match buyers and sellers. This works well for liquid markets, but fails for illiquid assets and is impractical on-chain due to high latency and gas costs. AMMs were invented to solve these problems (using math and pooled liquidity to enable permissionless, always-on trading for any token pair, without the need for order books or market makers).
1. What is an Automated Market Maker (AMM)?
Automated Market Makers (AMMs) are the backbone of decentralized exchanges (DEXs) like Uniswap, SushiSwap, and Balancer. Unlike traditional exchanges that use order books to match buyers and sellers, AMMs use smart contracts and mathematical formulas to set prices and create token pools. Anyone can trade or provide liquidity, permissionlessly, at any time.
How it works:
- Users trade against a pool of tokens (liquidity pool), not directly with other traders.
- Prices are determined by a mathematical formula, not by matching orders.
Why it matters:
- AMMs make DeFi trading permissionless, always-on, and accessible to anyone with a wallet.
 Figure: The essence of AMMs: liquidity pools, permissionless trading, and on-chain pricing.
Figure: The essence of AMMs: liquidity pools, permissionless trading, and on-chain pricing.
2. The Constant Product Formula (x*y=k) Explained
The most popular AMM model is the constant product market maker (CPMM), used by Uniswap v2 and many others.
Formula:
x * y = k
x= reserve of token X (e.g., ETH)y= reserve of token Y (e.g., USDC)k= constant (the product of reserves, must not decrease during swaps)
What does this mean?
- When you swap one token for another, you change the reserves, but the product (k) stays the same.
- The more you buy of one token, the more expensive it gets (slippage/price impact).
Key properties:
- Guaranteed liquidity: You can always trade, but the price gets worse for large trades.
- No order book needed: All pricing is on-chain and automatic.
3. Geometric Intuition: The AMM Curve
The equation x*y=k describes a hyperbola in the first quadrant. Every possible state of the pool is a point on this curve.

- Each trade shifts the pool’s reserve balances along the constant product curve, changing the token ratio and therefore the price.
- Spot price: Slope of the tangent at a point (
y/x). (At the initial state, this isy₀/x₀.) - Execution price: Average price over a finite trade (secant line between start/end points).
Key insight: The curve ensures you can never drain the pool (prices become extreme as reserves approach zero).
4. Price Impact, Slippage, and Impermanent Loss
⚠️ Slippage (User Risk)
- Definition: The difference between the expected price shown when you submit the trade and the actual price when it executes.
- Causes:
- Price Impact (explained below)
- Other pending trades (submitted before yours but mined first)
- Network delays, MEV, or bot front-running
- Mitigation: Most DEXs let you set a slippage tolerance. If the final price exceeds this threshold, the transaction reverts.
📉 Price Impact (a component of slippage)
- Definition: The price movement caused directly by your own trade due to the AMM curve.
- Why it happens: In AMMs like Uniswap, token prices are determined by a curve (x * y = k). Larger trades push further along the curve, worsening the price.
- Tip: Deeper liquidity = less price impact.
💸 Impermanent Loss (LP risk)
- Definition: The loss LPs experience compared to simply holding both tokens, if prices diverge.
- Why it happens: Arbitrageurs rebalance the pool when external prices move, leaving LPs with more of the losing asset.
- Formula for 50/50 pools:
IL = 2 * sqrt(price_ratio) / (1 + price_ratio) - 1 - Example: If ETH doubles vs. USDC, LPs lose ~5.7% vs. HODLing.
Read the full Impermanent Loss Guide →
5. Swap Math: Deriving the Output Formula
When you swap tokens in an AMM, the output amount is determined by the constant product formula, taking fees into account. Here's how it works:
Step-by-Step Swap Math
Suppose you swap Δx of token X for token Y:
- Initial reserves:
x₀ * y₀ = k - After swap:
(x₀ + Δx) * (y₀ - Δy) = k - Solve for output amount (
Δy):Δy = y₀ - (k / (x₀ + Δx))
With Fees (e.g., 0.3%)
- Only a portion of
Δxis used for the swap:Δxₑₓₑc = Δx * 0.997 - Output formula:
whereamountOut = (reserveOut * amountInWithFee) / (reserveIn + amountInWithFee)amountInWithFee = amountIn * 0.997(for a 0.3% fee)
Spot Price vs. Execution Price
- Spot price: Slope of the tangent at a point (
y/x). (At the initial state, this isy₀/x₀.) - Execution price: Average price over a finite trade (secant line between start/end points).
- Price impact: The difference between spot and execution price increases with trade size.
Example
Suppose the pool has 10 ETH and 20,000 USDC (reserveIn = 10, reserveOut = 20,000).
You want to swap 1 ETH for USDC.
- Calculate
amountInWithFee = 1 * 0.997 = 0.997 - Plug into the formula:
amountOut = (20,000 * 0.997) / (10 + 0.997) ≈ 1,814.6 USDC - After the swap, the reserves update, and the price changes according to the curve.
This formula ensures the product of reserves stays (almost) constant, minus the fee, and is the core of how AMMs like Uniswap work.
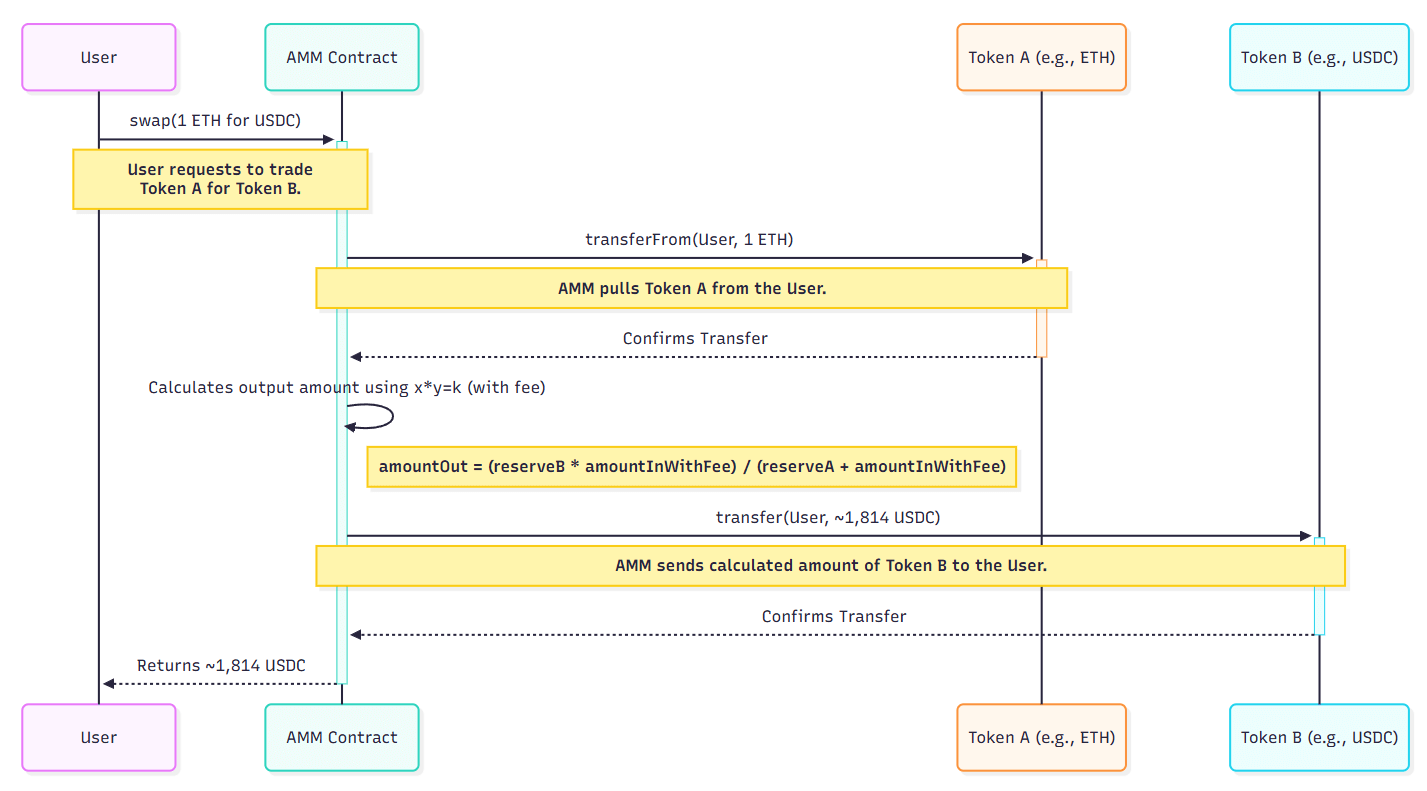 Figure: The core swap process in an AMM, from input to output calculation.
Figure: The core swap process in an AMM, from input to output calculation.
6. LP Tokens & Liquidity Math
Adding Liquidity
- First LP: Sets the initial price. Receives LP tokens =
sqrt(amount0 * amount1) - Subsequent LPs: Must deposit tokens in the current pool ratio. Receives LP tokens proportional to their share.
Removing Liquidity
- Burn LP tokens to withdraw a proportional share of both reserves.
Why LP Token Math Matters
- Prevents donation attacks (a technique where tokens are sent directly to the pool contract, potentially disrupting its internal accounting and pricing).
- Ensures fair share of pool for all LPs.
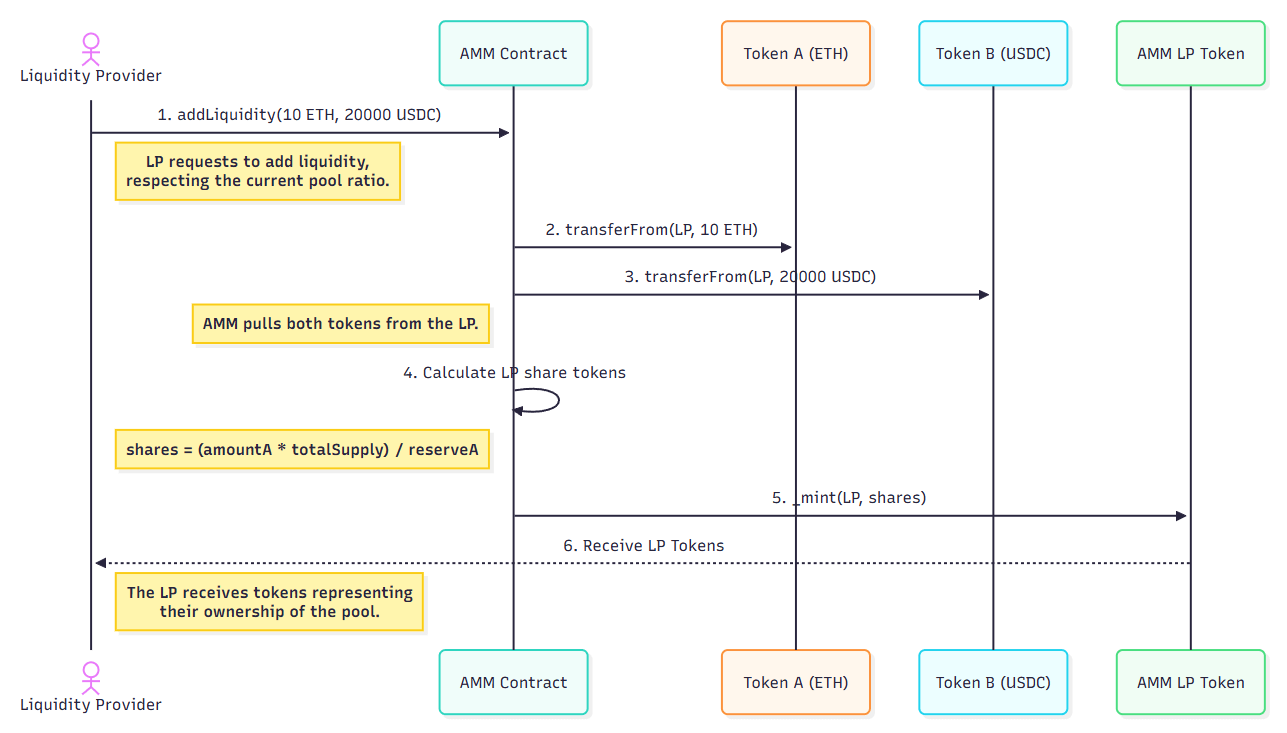 Figure: Adding liquidity to an AMM and receiving LP tokens in return.
Figure: Adding liquidity to an AMM and receiving LP tokens in return.
7. Solidity Code Walkthrough: Swap, Add, Remove Liquidity
Minimal AMM Contract (Swap, Add, Remove)
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.20;
import "@openzeppelin/contracts/token/ERC20/IERC20.sol";
import "@openzeppelin/contracts/token/ERC20/ERC20.sol";
contract MinimalAMM is ERC20 {
IERC20 public immutable token0;
IERC20 public immutable token1;
uint public reserve0;
uint public reserve1;
constructor(address _token0, address _token1) ERC20("AMM LP", "AMMLP") {
token0 = IERC20(_token0);
token1 = IERC20(_token1);
}
function swap(uint amountIn, address tokenIn, uint amountOutMin) external returns (uint amountOut) {
require(amountIn > 0, "Zero input");
require(tokenIn == address(token0) || tokenIn == address(token1), "Invalid token");
(IERC20 input, IERC20 output, uint reserveIn, uint reserveOut) =
tokenIn == address(token0) ? (token0, token1, reserve0, reserve1) : (token1, token0, reserve1, reserve0);
input.transferFrom(msg.sender, address(this), amountIn);
uint amountInWithFee = amountIn * 997 / 1000;
amountOut = (reserveOut * amountInWithFee) / (reserveIn + amountInWithFee);
require(amountOut >= amountOutMin, "Slippage");
output.transfer(msg.sender, amountOut);
// Update reserves
reserve0 = token0.balanceOf(address(this));
reserve1 = token1.balanceOf(address(this));
}
function addLiquidity(uint amount0Desired, uint amount1Desired) external returns (uint shares) {
uint amount0;
uint amount1;
if (reserve0 == 0 && reserve1 == 0) {
amount0 = amount0Desired;
amount1 = amount1Desired;
} else {
uint amount1Optimal = (amount0Desired * reserve1) / reserve0;
if (amount1Optimal <= amount1Desired) {
amount0 = amount0Desired;
amount1 = amount1Optimal;
} else {
uint amount0Optimal = (amount1Desired * reserve0) / reserve1;
amount0 = amount0Optimal;
amount1 = amount1Desired;
}
}
token0.transferFrom(msg.sender, address(this), amount0);
token1.transferFrom(msg.sender, address(this), amount1);
if (totalSupply() == 0) {
shares = sqrt(amount0 * amount1);
} else {
shares = (amount0 * totalSupply()) / reserve0;
}
require(shares > 0, "Insufficient shares");
_mint(msg.sender, shares);
reserve0 = token0.balanceOf(address(this));
reserve1 = token1.balanceOf(address(this));
}
function removeLiquidity(uint shares) external returns (uint amount0, uint amount1) {
require(shares > 0, "Zero shares");
amount0 = (reserve0 * shares) / totalSupply();
amount1 = (reserve1 * shares) / totalSupply();
require(amount0 > 0 && amount1 > 0, "Insufficient liquidity");
_burn(msg.sender, shares);
reserve0 = token0.balanceOf(address(this));
reserve1 = token1.balanceOf(address(this));
token0.transfer(msg.sender, amount0);
token1.transfer(msg.sender, amount1);
}
function sqrt(uint y) internal pure returns (uint z) {
if (y > 3) {
z = y;
uint x = y / 2 + 1;
while (x < z) {
z = x;
x = (y / x + x) / 2;
}
} else if (y != 0) {
z = 1;
}
}
}
- Security tip: Always follow the Checks-Effects-Interactions pattern and use OpenZeppelin's libraries for production.
8. Security Patterns & Best Practices
- Checks-Effects-Interactions (CEI): Update state before external calls to prevent reentrancy.
- Reentrancy: AMMs are less vulnerable, but always use CEI and consider OpenZeppelin's
ReentrancyGuardfor complex logic. - Math precision: Use integer math, avoid overflows, and use proven math libraries (see Uniswap's
Math.sol). - Fee-on-transfer tokens: Production AMMs handle these edge cases (test with non-standard ERC20s).
9. AMM Model Comparisons
| Model | Formula | Curve | Use Case | Trade-Offs |
|---|---|---|---|---|
| CPMM | x*y=k | Hyperbola | General token swaps | High slippage for large trades |
| Constant Sum | x+y=k | Linear | Stablecoin swaps | No liquidity if price deviates from 1:1 |
| Constant Mean | (∏xᵢ^wᵢ) = k | Multi-dim | Multi-asset pools | Complex math, flexible weights |
| Hybrid | Combo | Flat/curve | Stablecoins (Curve) | Low slippage, reverts to CPMM if depegged |
When to use each model:
- CPMM (x*y=k): Best for general-purpose token swaps, especially when you want guaranteed liquidity for any pair. Downside: high slippage for large trades.
- Constant Sum (x+y=k): Ideal for stablecoin-to-stablecoin swaps where you want zero slippage near 1:1, but beware: one side can be drained if price moves.
- Constant Mean: Used by Balancer for multi-asset pools with custom weights (e.g., 80/20). Great for portfolio management, but math and impermanent loss are more complex.
- Hybrid (Curve/StableSwap): Combines CPMM and constant sum for low-slippage swaps between tightly correlated assets (e.g., stablecoins). Reverts to CPMM if prices depeg.
10. Advanced Risks: Oracles, Front-Running, Sandwich Attacks
- Oracle manipulation: Never use spot price as an oracle. Use TWAPs (time-weighted average price) or Chainlink.
- Front-running & Sandwich Attacks: Bots can see your trade in the mempool and trade before/after you. Use tight slippage and private relays (Flashbots) to reduce risk.
Read the Flash Loan Exploits Guide →
 Figure: Managing risks in decentralized exchanges: slippage, impermanent loss, and liquidity depth.
Figure: Managing risks in decentralized exchanges: slippage, impermanent loss, and liquidity depth.
11. Concentrated Liquidity & The Evolution of AMMs
- Uniswap v3 introduced concentrated liquidity, letting LPs allocate capital within chosen price ranges. This improves capital efficiency and fee potential but comes with tradeoffs:
- LPs must actively manage positions to stay in range.
- When the price moves outside the range, liquidity becomes one-sided (held entirely in one asset), earning no fees and increasing impermanent loss risk compared to v2.
- Stablecoin AMMs (Curve, Balancer): Use different math for low-slippage swaps between similar assets.
- Capital efficiency: CPMMs are simple but inefficient; new models let LPs focus capital where it's most useful.
12. Economic & Game Theory Insights
- Arbitrage: Essential for keeping AMMs in sync with global prices, but causes impermanent loss for LPs. Arbitrageurs buy the underpriced asset from the AMM and sell it on the open market, pushing the AMM price back in line. This process is what realizes impermanent loss for LPs.
- Loss-versus-rebalancing (LVR): The value extracted by arbitrageurs is the LP's loss vs. HODLing. This is a fundamental tradeoff: LPs earn fees, but pay for it by being "short volatility" (they lose if prices diverge too much).
- LPs are short volatility: They earn fees but lose if prices diverge too much. Providing liquidity is like selling options: you profit in stable markets, but lose if prices move sharply.
13. Practical Tips for Builders & LPs
- Understand the math: Know how price impact and impermanent loss work before providing liquidity.
- Use audited code: Always use OpenZeppelin and proven AMM templates.
- Monitor your positions: Track fees earned vs. potential impermanent loss.
- Test with non-standard tokens: Some ERC20s have transfer fees or non-standard logic.
- Stay updated: DeFi evolves fast, follow new AMM models and security best practices.
14. The Power and Tradeoffs of AMMs
AMMs revolutionized DeFi by making on-chain trading and liquidity provision simple and permissionless. But their math creates new risks (price impact, impermanent loss, and arbitrage). By understanding the constant product formula and using secure, well-audited code, you can trade and build confidently in the world of decentralized finance.
Ready to build or test your own AMM? Try the Minimum Viable Exchange (Dex) Challenge!
Want to learn more about LP risks? Read the Impermanent Loss Guide!